Histoires de Mathématiques
Analyse

L'homme qui savait l'infini
approximations de pi
Le nombre incroyable de théorèmes énoncés par Ramanujan, la bizarrerie apparente de beaucoup de ses formules, ont pu laisser penser à une intuition surnaturelle. C'est le cas en particulier pour les approximations de Pi. En fait ces résultats ont des racines historiques profondes, qui remontent à Euler, Wallis, Viète, et même Archimède. Voir aussi
 Quadrateurs de cercle
Quadrateurs de cercle
 Euler et l'analyse
Euler et l'analyse
public : lycéens et étudiants
Personnages ►

John Wallis
1616 — 1703
Le plus grand mathématicien anglais avant Newton
 Newton et l'analyse infinitésimale
Newton et l'analyse infinitésimale

Leonhard Euler
1707 — 1783
Lisez-le, il est notre maître à tous
 Recettes, algorithmes et mathématiques
Recettes, algorithmes et mathématiques

François Viète
1540 — 1603
L'inventeur de l'algèbre symbolique était aussi cryptanalyste
 Viète, cryptographie et algèbre
Viète, cryptographie et algèbre

Eudoxe de Cnide
c. -390 — c. -337
La méthode d'exhaustion et la première théorie grecque des planètes
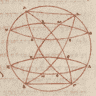 Géométrie et astronomie en Grèce
Géométrie et astronomie en Grèce

Archimède
-287 — -212
Le plus grand des mathémaiciens, selon tous ceux qui ont suivi
 Le tangram d'Archimède
Le tangram d'Archimède

Bertrand Russell
1872 — 1970
Un grand logicien, auteur d'un paradoxe troublant
 Logique de Frege et Russell
Logique de Frege et Russell
Textes ►

A treatise of Algebra
John Wallis 1685
Le premier traitement pédagogique de l'algèbre, avec en plus la première perspective historique
 Calculs de racines
Calculs de racines
 Quadratures d'Archimède
Quadratures d'Archimède
 Équation de Pell-Fermat
Équation de Pell-Fermat
 Combinatoire d'un vers latin
Combinatoire d'un vers latin
 Harriot entre Viète et Descartes
Harriot entre Viète et Descartes
 Localisation des racines d'équations
Localisation des racines d'équations
 Représentation géométrique des complexes
Représentation géométrique des complexes
 Mathématiques de Ramanujan
Mathématiques de Ramanujan
référence : Wallis (1685) A treatise of Algebra, London : Playford
source : Google books

Introduction à l'Analyse Infinitésimale, Tome premier
Leonhard Euler 1748 (édition de 1835)
La traduction du livre majeur d'Euler sur sa théorie des fonctions
 Euler contre Voltaire
Euler contre Voltaire
 Astronomie indienne
Astronomie indienne
 Oresme et la représentation des fonctions
Oresme et la représentation des fonctions
 Représentation géométrique des complexes
Représentation géométrique des complexes
 Cordes vibrantes
Cordes vibrantes
 Bolzano, Cauchy et la rigueur
Bolzano, Cauchy et la rigueur
 Série du binôme de Newton
Série du binôme de Newton
référence : Euler (1835) Introduction à l'Analyse Infinitésimale, Tome premier, trad. : J. B. Labey, Paris : Bachelier
source : Internet Archive

Introduction à l'Analyse Infinitésimale, Tome second
Leonhard Euler 1748 (édition de 1835)
La traduction du livre majeur d'Euler sur sa théorie des fonctions
 Euler contre Voltaire
Euler contre Voltaire
 Astronomie indienne
Astronomie indienne
 Oresme et la représentation des fonctions
Oresme et la représentation des fonctions
 Représentation géométrique des complexes
Représentation géométrique des complexes
 Cordes vibrantes
Cordes vibrantes
 Bolzano, Cauchy et la rigueur
Bolzano, Cauchy et la rigueur
 Série du binôme de Newton
Série du binôme de Newton
référence : Euler (1835) Introduction à l'Analyse Infinitésimale, Tome second, trad. : J. B. Labey, Paris : Bachelier
source : Internet Archive

