La continuité des intensités

vers le concept de fonction

L'ancêtre de la notion de fonction est à chercher dans les mouvements, en particulier astronomiques. Les Grecs manipulaient toutes sortes de courbes géométriques issues de mouvements, sans y voir nécessairement des fonctions du temps à notre sens. Oresme a compris le premier que n'importe quelle quantité variable pouvait être représentée par une suite de longueurs. À partir du dix-septième siècle, l'intérêt s'est déplacé de la géométrie vers l'algèbre, et jusqu'à la fin du dix-huitième, les fonctions étaient vues comme des expressions algébriques contenant la variable. Ce n'est qu'au dix-neuvième que la notion de fonction telle que nous la connaissons s'est développée. Voir aussi Astronomie mésopotamienne Théorème de Merton et mouvement accéléré 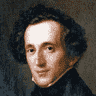Séries trigonométriques

public : lycéens et étudiants

fichier pdf  ►