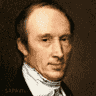Histoires de Mathématiques
Astronomie

Les trois corps
héritiers de Newton
Newton a laissé à ses héritiers, Euler, d'Alembert, Laplace, Gauss, un champ énorme à défricher. Il avait donné le principal, la gravitation universelle et la manière d'en déduire un système d'équations différentielles. Mais il n'avait pas caché la difficulté d'implémentation, dans la situation réelle où plus de deux corps étaient en interaction. La recherche sur ce problème allait occuper l'essentiel des dix-huitième et dix-neuvième siècles, et au passage donner naissance à nombre de méthodes, toujours en vigueur en analyse numérique. Voir aussi
 Newton et l'analyse numérique
Newton et l'analyse numérique
 Newton et l'analyse infinitésimale
Newton et l'analyse infinitésimale
public : tous
Personnages ►

Isaac Newton
1643 — 1727
Comment citer tous les domaines qu'il a révolutionnés ?
 Newton et l'analyse numérique
Newton et l'analyse numérique

Pierre-Simon Laplace
1749 — 1827
La théorie des probabilités n'était rien par rapport à sa mécanique
céleste
 Laplace et les probabilités
Laplace et les probabilités

Carl Gustav Jacobi
1804 — 1851
Un jeune mathématicien prometteur dans la génération d'après Gauss
 Gauss et l'arithmétique complexe
Gauss et l'arithmétique complexe
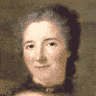
Émilie du Châtelet
1706 — 1749
Pourquoi ne serait-elle que la maîtresse de Voltaire ?
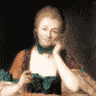 Émilie du Châtelet
Émilie du Châtelet
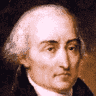
Joseph-Louis Lagrange
1736 — 1813
Le plus grand des successeurs d'Euler
 Le repos philosophique de Lagrange
Le repos philosophique de Lagrange

James Gregory
1638 — 1675
Il a participé à la naissance du calcul différentiel
 Développements en série
Développements en série

Adrien-Marie Legendre
1752 — 1833
Se retrouver en compétition avec Gauss, c'était manquer de chance
 Somme des angles d'un triangle
Somme des angles d'un triangle

Leonhard Euler
1707 — 1783
Lisez-le, il est notre maître à tous
 Recettes, algorithmes et mathématiques
Recettes, algorithmes et mathématiques
Textes ►

Principes Mathématiques de la Philosophie Naturelle, Tome Premier
Isaac Newton 1687 (édition de 1759)
La traduction commentée des Principia de Newton, par Émilie du Châtelet
 Newton et l'analyse numérique
Newton et l'analyse numérique
 Tourbillons de Descartes
Tourbillons de Descartes
 Cardan, Newton et l'alchimie
Cardan, Newton et l'alchimie
 Newton contre Leibniz
Newton contre Leibniz
 Émilie du Châtelet
Émilie du Châtelet
 Femmes et calculs astronomiques
Femmes et calculs astronomiques
 De Moivre et les probabilités
De Moivre et les probabilités
 Problème des trois corps
Problème des trois corps
 Grassmann et les vecteurs
Grassmann et les vecteurs
référence : Newton (1759) Principes Mathématiques de la Philosophie Naturelle, Tome Premier, trad. : Émilie du Châtelet, Paris : Desaint et Saillant
source : Google books

Principes Mathématiques de la Philosophie Naturelle, Tome Second
isaac Newton 1687 (édition de 1759)
La traduction des Principia de Newton, par Émilie du Châtelet
 Newton et l'analyse numérique
Newton et l'analyse numérique
 Tourbillons de Descartes
Tourbillons de Descartes
 Cardan, Newton et l'alchimie
Cardan, Newton et l'alchimie
 Newton contre Leibniz
Newton contre Leibniz
 Émilie du Châtelet
Émilie du Châtelet
 Femmes et calculs astronomiques
Femmes et calculs astronomiques
 De Moivre et les probabilités
De Moivre et les probabilités
 Problème des trois corps
Problème des trois corps
 Grassmann et les vecteurs
Grassmann et les vecteurs
référence : Newton (1759) Principes Mathématiques de la Philosophie Naturelle, Tome Second, trad. : Émilie du Châtelet, Paris : Desaint et Saillant
source : Google books

Mouvement des Corps Célestes Parcourant des Sections Coniques Autour du Soleil
Carl Friedrich Gauss 1809 (édition de 1864)
Dans ce livre apparaissent la loi normale, le principe des moindres carrés, ainsi que l'usage moderne du mot algorithme
 Loi de Gauss, statistique et astronomie
Loi de Gauss, statistique et astronomie
 Cheminement du mot algorithme
Cheminement du mot algorithme
 Problème des trois corps
Problème des trois corps
référence : Gauss (1864) Théorie du Mouvement des Corps Célestes Parcourant des Sections Coniques Autour du Soleil, trad. : E. Dubois, Paris : Bertrand
source : Gallica